A análise de dados de vida de confiabilidade refere-se ao estudo e modelagem da vida dos produtos observados. Os dados de vida útil podem ser a vida útil dos produtos no mercado, como o tempo em que o produto operou com sucesso ou o tempo em que o produto operou antes de falhar. Esses tempos de vida podem ser medidos em horas, quilômetros, ciclos até a falha, ciclos de estresse ou qualquer outra métrica com a qual a vida ou exposição de um produto possa ser medida. Todos esses dados de vida útil do produto podem ser englobados nos dados de vida útil ou, mais especificamente, dados de vida útil do produto. A análise e previsão subsequentes são descritas como análise de dados de vida. Para os propósitos desta referência, limitaremos nossos exemplos e discussões aos tempos de vida de objetos inanimados, como equipamentos, componentes e sistemas aplicados à engenharia de confiabilidade, porém os mesmos conceitos podem ser aplicados em outras áreas.
Uma visão geral dos conceitos básicos
Ao realizar a análise de dados de vida (também comumente chamada de análise Weibull), o profissional tenta fazer previsões sobre a vida de todos os produtos produzidos, ajustando uma distribuição estatística (modelo) aos dados de vida de uma amostra representativa de unidades. A distribuição parametrizada para o conjunto de dados pode então ser usada para estimar características importantes da vida útil do produto, como confiabilidade ou probabilidade de falha em um momento específico, a vida média e a taxa de falha. A análise de dados de vida exige que o profissional:
- Reúna dados de vida para o produto.
- Selecione uma distribuição de vida útil que se ajuste aos dados e modele a vida útil do produto.
- Estime os parâmetros que ajustarão a distribuição aos dados.
- Gere gráficos e resultados que estimam as características de vida do produto, como a confiabilidade ou a vida média.
Distribuições de vida (modelos de dados de vida)
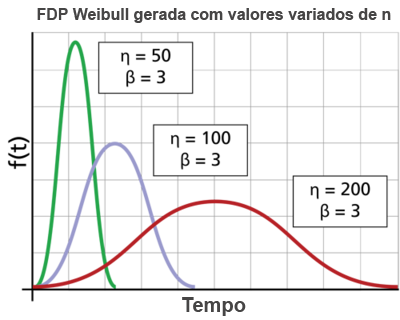
As distribuições estatísticas foram formuladas por estatísticos, matemáticos e engenheiros para modelar matematicamente ou representar determinado comportamento. A função densidade de probabilidade (fdp) é uma função matemática que descreve a distribuição. A fdp pode ser representada matematicamente ou em um gráfico onde o eixo x representa o tempo, conforme mostrado a seguir.
A fdp Weibull de 3 parâmetros é dada por:
Onde:
e:
Algumas distribuições, como Weibull e lognormal, tendem a representar melhor os dados de vida e são comumente chamadas de "distribuições do tempo de vida" ou "distribuições de vida". De fato, a análise de dados de vida às vezes é chamada de "análise de Weibull" porque a distribuição de Weibull, formulada pelo professor Waloddi Weibull, é uma distribuição popular para analisar dados de vida. O modelo Weibull pode ser aplicado de várias formas (incluindo Weibull de 1 parâmetro, 2 parâmetros, 3 parâmetros ou misto). Outras distribuições de vida comumente usadas incluem as distribuições exponencial, lognormal e normal. O analista escolhe a distribuição de vida mais apropriada para modelar cada conjunto de dados específico com base na experiência anterior e nos testes de ajuste.
Estimativa de parâmetros
Para ajustar um modelo estatístico a um conjunto de dados de vida, o analista estima os parâmetros da distribuição de vida que farão com que a função se ajuste melhor aos dados. Os parâmetros controlam a escala, forma e localização da fdp . Por exemplo, no modelo Weibull de 3 parâmetros (mostrado acima), o parâmetro de escala, η, define onde está a maior parte da distribuição. O parâmetro de forma, β, define a forma da distribuição e o parâmetro de localização, γ, define a localização da distribuição no tempo.
Vários métodos foram desenvolvidos para estimar os parâmetros que se ajustarão a uma distribuição de tempo de vida para um determinado conjunto de dados. Alguns métodos de estimativa de parâmetros disponíveis incluem plotagem de probabilidade, regressão de classificação em x (RRX), regressão de classificação em y (RRY) e estimativa de máxima verossimilhança (MLE). O método de análise apropriado irá variar dependendo do conjunto de dados e, em alguns casos, da distribuição de vida selecionada.
Resultados e gráficos calculados
Depois de calcular os parâmetros para ajustar uma distribuição de vida a um conjunto de dados específico, você pode obter uma variedade de gráficos e resultados calculados da análise, incluindo:
- Confiabilidade em tempo determinado: A probabilidade de uma unidade operar com sucesso em um determinado ponto no tempo. Por exemplo, há 88% de chance de que o produto funcione com sucesso após 3 anos de operação.
- Probabilidade de falha em tempo determinado: A probabilidade de uma unidade falhar em um determinado momento. A probabilidade de falha também é conhecida como "não confiabilidade" e é o recíproco da confiabilidade. Por exemplo, há 12% de chance de a unidade falhar após 3 anos de operação (probabilidade de falha ou falta de confiabilidade) e 88% de chance de operar com sucesso (confiabilidade).
- Vida média: O tempo médio que as unidades na população devem operar antes da falha. Essa métrica é frequentemente chamada de "tempo médio até a falha" do mean time to failure (MTTF) ou "tempo médio antes da falha" do mean time between failures (MTBF).
- Taxa de falhas: O número de falhas por unidade de tempo que podem ocorrer para o produto.
- Tempo de garantia: O tempo estimado em que a confiabilidade será igual a uma meta especificada. Por exemplo, o tempo estimado de operação é de 4 anos para uma confiabilidade de 90%.
- B(X) life: O tempo estimado em que a probabilidade de falha atingirá um ponto especificado (X%). Por exemplo, espera-se que 10% dos produtos falhem em 4 anos de operação, a vida útil B(10) é de 4 anos. (Observe que isso equivale a um tempo de garantia de 4 anos para uma confiabilidade de 90%.)
- Gráfico de probabilidade: Um gráfico da probabilidade de falha ao longo do tempo. (Observe que os gráficos de probabilidade são baseados na linearização de uma distribuição específica. Consequentemente, a forma de um gráfico de probabilidade para uma distribuição será diferente da forma para outra. Por exemplo, um gráfico de probabilidade de distribuição exponencial tem eixos diferentes daqueles de um gráfico de probabilidade de distribuição normal.)
- Confiabilidade vs. gráfico de tempo: Um gráfico da confiabilidade ao longo do tempo.
- Gráfico fdp: Um gráfico da função densidade de probabilidade (fdp).
- Taxa de falha vs. gráfico de tempo: Um gráfico da taxa de falha ao longo do tempo.
- Gráfico de contorno: Uma representação gráfica das soluções possíveis para a equação da razão de verossimilhança. Isso é empregado para fazer comparações entre dois conjuntos de dados diferentes.
Limites de Confiança
Como os resultados da análise de dados de vida são estimativas baseadas nos tempos de vida observados de uma amostragem de unidades, há incerteza nos resultados devido ao tamanho limitado da amostra. Os "limites de confiança" (também chamados de "intervalos de confiança") são usados para quantificar essa incerteza devido ao erro de amostragem, expressando a confiança de que um intervalo específico contém a quantidade de interesse. Se um intervalo específico contém ou não a quantidade de interesse é desconhecido.
Os limites de confiança podem ser expressos como bilaterais ou unilaterais. Os limites bilaterais são usados para indicar que a quantidade de interesse está contida nos limites com uma confiança específica. Os limites unilaterais são usados para indicar que a quantidade de interesse está acima do limite inferior ou abaixo do limite superior com uma confiança específica. O tipo apropriado de limites depende do aplicativo. Por exemplo, o analista usaria um limite inferior unilateral na confiabilidade, um limite superior unilateral para porcentagem de falhas na garantia e limites laterais nos parâmetros da distribuição. (Observe que os limites unilateral e bilateral estão relacionados. Por exemplo, o limite bilateral 90% inferior é o limite unilateral 95% inferior e o limite bilateral superior 90% é o limite unilateral superior 95% limite unilateral superior.)
| Traduzido e publicado sob licença Creative Commons |  |
ReliaWiki |










